È da tempo che mi "sbattevo" per un problema di questo tipo. Si trova poca documentazione in realtà (almeno in Italiano), per farla breve, partendo da un metodo numerico per risolvere un'equazione differenziale (tramite elementi finiti, differenze finite, ecc) possiamo applicare delle leggi di conservazione (su base fisica o matematica) per avere un ulteriore controllo dell'errore e compensarlo, correggere il risultato numerico. Questa procedura in matematica si chiama "mimesis" e la sigla MFDM indica Mimetic Finite Difference Methods, ciò che ho applicato io.
Nel mio caso d'esempio, sono partito dalla legge della diffusione, classica Heat Equation 1D (che in un altro esempio avevo risolto col più semplice FTCS e poi BTCS).
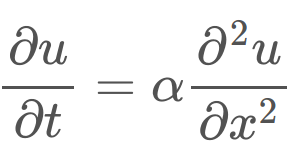
Al di là poi dei parametri fisici, ci ho messo dentro dei numeri come condizioni iniziali e parametri del problema (avendo poi applicato un metodo in forma implicita, BTCS con CC periodiche, non occorre nemmeno la condizione vincolo sul passo di discretizzazione), ciò che mi interessava era questo passaggio concettuale, che diciamo, è stata un pochino una mia interpretazione: la conservazione della grandezza fisica, diciamo "massa termica", se è un sistema isolato, conserviamo il totale della temperatura nel dominio. Quindi, il mio ragionamento:
- ad ogni iterazione, il metodo numerico produce certamente un errore
- se sommiamo le celle del dominio ad ogni iterazione abbiamo l'errore totale (noto, dato che il totale della grandezza abbiamo detto che si deve conservare)
- quindi l'errore ad ogni step sarà dato dalla differenza fra questi due valori
- assumendo distribuzione uniforme dell'errore (non sarà perfetto - dipende dal problema specifico -, ma è pur sempre un più accurato metodo di compensazione dell'errore piuttosto che non fare nulla), "aggiusto" i valori di ogni cella aggiungendo lo scarto medio per ognuno (errore totale diviso il numero di celle totali), quindi
u+=1.0/Nx*(initial_mass-current_mass)
Ecco tutto il codice Python del programma:
# MFDM, Heat Equation 1D, con legge di conservazione
import numpy as np
import matplotlib.pyplot as plt
import random
L = 1.0 # Lunghezza del dominio
T = 1.0 # Tempo finale
D = 0.01 # Diffusività termica
Nx = 50 # Numero di punti spaziali
Nt = 500 # Numero di punti temporali
dx = L / (Nx - 1)
dt = T / (Nt - 1)
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
# Condizioni iniziali con distribuzione gaussiana
u = np.exp(-100 * (x - 0.5)**2)
delta = D * dt / dx**2 # Parametro di stabilità
# Matrice di coefficienti per le differenze finite mimetiche
A = np.zeros((Nx, Nx))
for i in range(Nx):
A[i, i] = 1 + 2 * delta
A[i, (i - 1) % Nx] = -delta
A[i, (i + 1) % Nx] = -delta
# Calcolo della massa totale iniziale
initial_mass = np.sum(u)
# Soluzione temporale
for n in range(1, Nt):
u_new = np.linalg.solve(A, u)
u = u_new
# Verifica della conservazione della massa
current_mass = np.sum(u)
print(f"Step {n}, Mass: {current_mass}, Initial Mass: {initial_mass}, e: {1.0/Nx*(initial_mass-current_mass)}")
u+=1.0/Nx*(initial_mass-current_mass)
# Visualizzazione dei risultati
plt.plot(x, u, label='Temperatura finale')
plt.xlabel('Posizione (x)')
plt.ylabel('Temperatura (u)')
plt.title('Soluzione dell\'equazione del calore 1D con differenze finite mimetiche')
plt.legend()
plt.show()
I valori finali dipendono dai parametri scelti, come detto, ciò che mi interessava era l'aspetto concettuale di questa procedura, che ho seguito in modo un po' "fai da te". Per questo caso di studio comunque i termini correttivi sono piuttosto piccoli (errore per ogni cella dell'ordine di 10-17). Vediamo come appare il risultato finale.
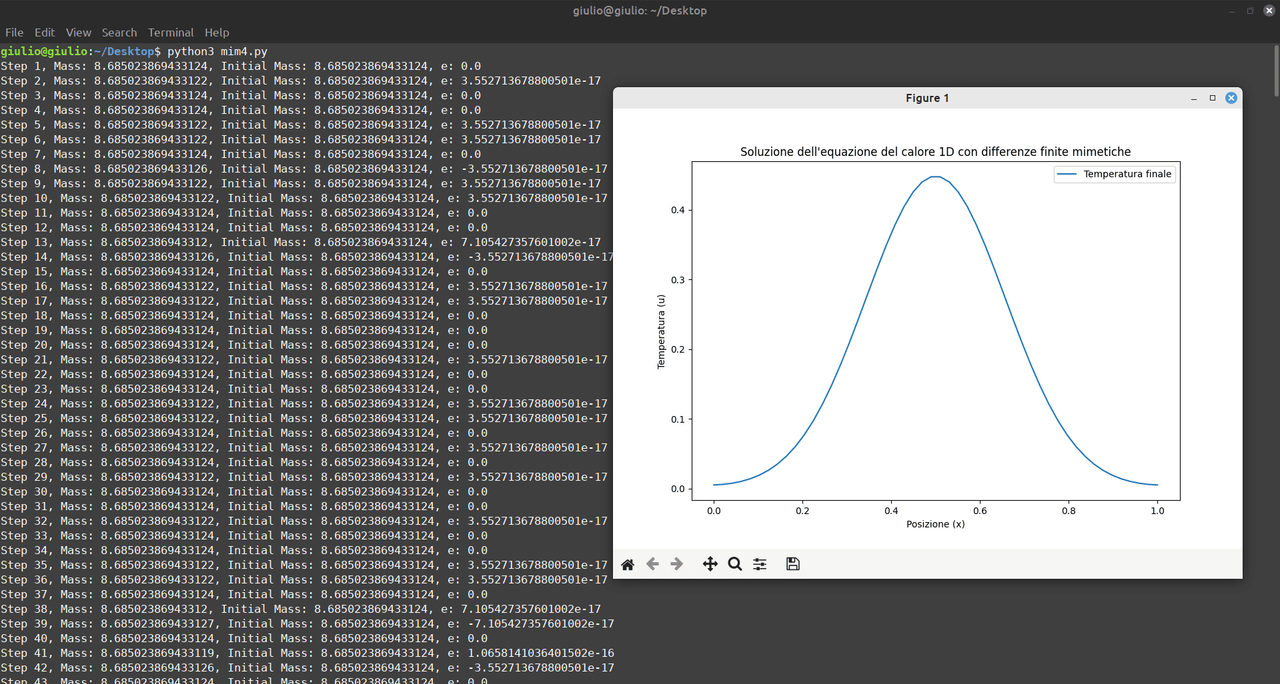
Cosa ne pensate, in particolare intendo dal punto di vista concettuale, di questo approccio un po' "fai da te", come compensazione dell'errore sulla base di una legge di conservazione? 🙂