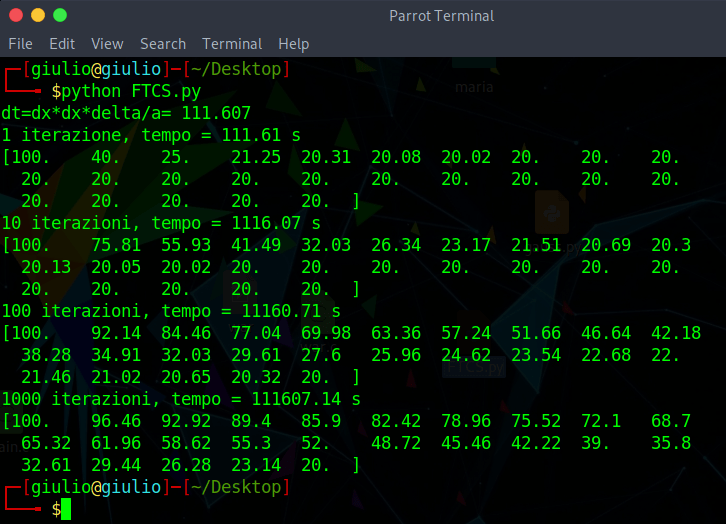
Riporto i risultati di un semplice esempio della Heat Equation di Fourier (equazione differenziale della diffusione del calore) in 1D, variabile nel tempo. Ho creato un programmino in Python, che poi metto come immagine.
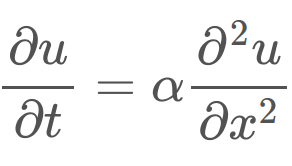
Ho usato questi dati:
- T0 = 100 °C
- a = diffusività termica = 2,24*10-5 m2/s (valore preso in letteratura, per l'aria)
- Tambiente = 20 °C
- dx = 0,1 m
- metodo numerico: differenze finite, FTCS, "forward in time, central in space"
- delta = passo di discretizzazione (metodo numerico) = 0,25 (condizione di stabilità FTCS 1D: delta≤0,5)
- ne consegue che: dt = 111,6 secondi
- condizioni al contorno: T0 nel punto (cella) iniziale, costante nel tempo, mentre nelle altre celle si ha Tambiente
- N = 25, quindi 25 celle, N*dx = 2,5 metri
Ho riportato il set di valori dopo un'iterazione (tempo = 111,6 secondi, quasi due minuti), 10 iterazioni (circa 19 minuti), 100 iterazioni (3 ore) e 1000 iterazioni (30 ore). Ovviamente come valore della diffusività termica è stato preso un valore molto molto molto piccolo, nella realtà la diffusione sarebbe maggiore anche perché entrano in gioco altri fattori. Vediamo comunque che dai set di dati all'inizio la prima cella è l'unica col valore più alto, col tempo (quindi col numero di iterazioni) si diffonde sempre di più anche alle altre celle. Ovviamente, come detto, sono stati presi valori solo come esempio, la diffusione nella realtà in genere sarebbe più rapida.
Altro commento: il metodo FTCS non è certo il più accurato, il più indicato, così come il passo di discretizzazione delta se si vogliono ottenere risultati più accurati, può essere preso più piccolo; le ragioni della mia scelta sono queste due:
- delta va bene così, perché non mi interessano 100 cifre decimali e risparmiamo costo computazionale
- ho scelto FTCS perché è di più facile implementazione rispetto ad altri es. BTCS (o la media fra questi due, metodo sicuramente più accurato), che richiedono ad ogni iterazione di trovare gli zeri di una funzione... metodo numerico implicito e non esplicito