In passato avevo trattato casi simili, Esempio Heat Equation 1D - Python - FTCS e poi Esempio diffusione inquinante in piscina - Python. Si tratta di partire da un'equazione differenziale, risolverla con un metodo numerico approssimato (analisi numerica), alle differenze finite; in entrambi i precedenti casi avevo usato FTCS (Forward in Time, Central in Space), relativamente semplice in quanto metodo esplicito.
Ho scritto ora un algoritmo diverso, volendo provare la variante di FTCS ovvero BTCS (Backward in Time, Central in Space) che è più complesso da gestire, nonostante poi abbia una serie di vantaggi di stabilità ecc, senza entrare troppo nei dettagli, si tratta comunque di un metodo implicito quindi risoluzione non immediata ma del tipo Ax=b (giusto come approfondimento vedi anche Metodo della bisezione per sistemi di equazioni). Non conoscevo bene alternative a questo, vedendo la matrice noto che è tridiagonale quindi in pratica significa questo, perché lavorare con operazioni su tutti i campi della matrice quando sono tutti nulli tranne quelli della diagonale principale e le due diagonali adiacenti (sopra e sotto)? Allora cercando, ho conosciuto questa alternativa, algoritmo di Thomas (algoritmo per matrici tridiagonali). Ha complessità O(N) mentre il metodo di eliminazione di Gauss o la decomposizione LU lavorano su tutti i termini della matrice e hanno complessità pari a O(N3). Questo significa che, raddoppiando N (dimensione della matrice, quindi la dimensione del dominio, o il livello di accuratezza spaziale), nel primo caso raddoppia il tempo di esecuzione mentre nel secondo caso aumenta di 23 quindi 8 volte!
Ho scelto di scrivere due programmini in Python, per semplicità poi nella rappresentazione grafica, certo il mio è un esempio, volendo essere più rigorosi anziché Python sarebbe computazionalmente molto più efficiente scriverlo in C (vedi anche: Python + C assieme con la libreria CFFI: efficienza top).
Comunque sia, nel mio caso ho considerato questo esempio: equazione della diffusione (può essere temperatura, concentrazione di una sostanza ecc, inseriamo noi i dati che vogliamo, la struttura matematica non cambia), in un caso risolta con la funzione linalg.solve() della libreria Numpy (risoluzione Ax=b tramite decomposizione LU, come già detto complessità O(N3)) e nel secondo caso risolto con l'algoritmo di Thomas quindi a fronte di un'implementazione iniziale, poi abbiamo complessità O(N), caso molto più favorevole se aumentassimo la dimensione del dominio quindi il numero di iterazioni. Come condizioni iniziali, valore nullo ovunque tranne un picco al centro (quello che abbiamo poi, iterando nel tempo, è un andamento diffusivo, curva gaussiana). Ho fatto un certo numero di iterazioni temporali (20000), quanto al dominio, nel primo caso ho messo una risoluzione più elevata (dx=0.01) mentre nel secondo caso dx=1. Non mi interessava particolarmente mostrare la differenza di tempo di esecuzione, dato che la sappiamo vista la differenza di andamento (O(N) vs O(N3)). Volevo invece mostrare i due algoritmi a confronto, come implementazione. Poi come detto, da questa implementazione di base funzionante, è possibile cambiare le condizioni iniziali, condizioni al contorno, a seconda di quello che abbiamo (diffusione termica? Diffusione di un inquinante? Eccetera).
Python: algoritmo Ax=b, linalg.solve(), equazione diffusione
Ecco tutto il codice:
#BTCS Ax=b
import numpy as np
from matplotlib import pyplot as plt
L=20
V0=100
delta=0.01
dx=0.1
D=0.1
dt=delta/D*dx**2
T=20
N=(int)(L/dx)
A=np.zeros((N,N))
X=np.zeros(N)
b=np.zeros(N)
b[(int)(N/2)]=V0
X=b
for j in range(N):
for i in range(N):
if i==j:
A[i][j]=1+2*delta
elif (i+1==j and i<N-1) or (i-1==j and i>0):
A[i][j]=-delta
else:
A[i][j]=0
for k in range((int)(T/dt)):
X=np.linalg.solve(A,b)
b=X
print("N iterazioni =",(int)(T/dt))
print("dt =",dt)
plt.figure()
for i in range(N):
plt.plot(i*dx,X[i],'o',color='blue')
plt.show()
Python: algoritmo di Thomas (matrici tridiagonali), equazione diffusione
Prima ri riportare il codice, vediamo come è strutturato all'inizio:

Ecco tutto il codice:
#Algoritmo di Thomas matrici tridiagonali
import numpy as np
from matplotlib import pyplot as plt
N=20
V0=100
delta=0.01
dx=1
D=0.1
dt=delta/D*dx**2
T=20
a=np.zeros(N)-delta # -delta
b=np.zeros(N)+1+2*delta # 1+2delta
c=np.zeros(N)-delta # -delta
d=np.zeros(N) # termine noto
d[(int)(N/2)]=V0
a[0]=0
c[N-1]=0
for k in range((int)(T/dt)):
for i in range(1,N):
if(i==0):
c[i]=c[i]/b[i]
d[i]=d[i]/b[i]
else:
c[i]=c[i]/(b[i]-a[i]*c[i-1])
d[i]=(d[i]-a[i]*d[i-1])/(b[i]-a[i]*c[i-1])
cont=N-2
while cont>=0:
d[cont]=d[cont]-c[cont]*d[cont+1]
cont=cont-1
print("N iterazioni =",(int)(T/dt))
print("dt =",dt)
plt.figure()
for i in range(N):
plt.plot(i,d[i],'o',color='blue')
plt.show()
Ecco infine un'immagine del risultato grafico.
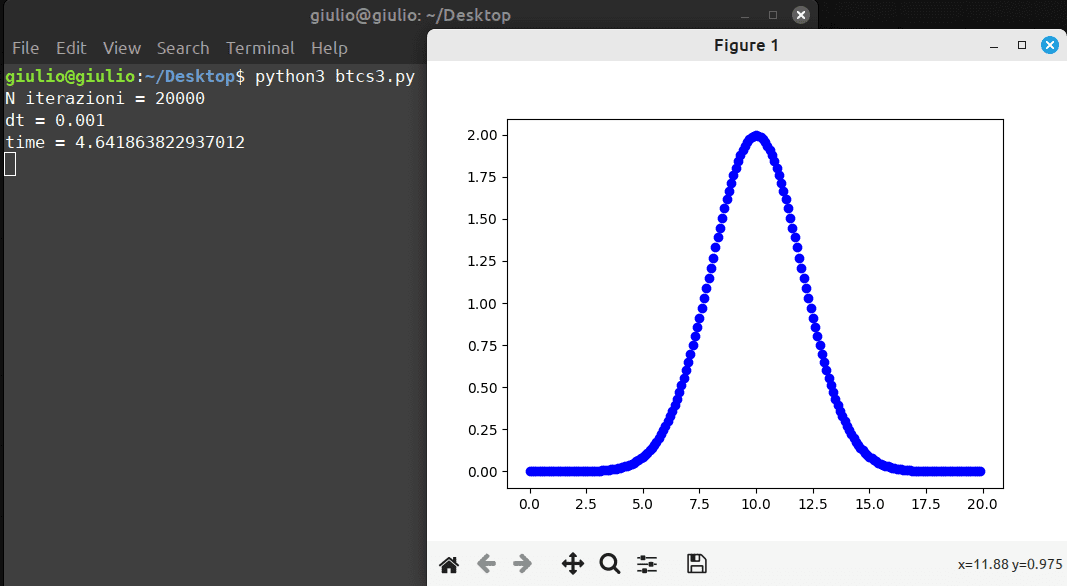
Vi piace l'idea? Conoscevate questi metodi numerici? 🙂