Ho pensato di risolvere un problemino di analisi numerica con il metodo del gradiente coniugato (conjugate gradient), un metodo di risoluzione di sistemi lineari con convergenza molto efficiente. Argomenti simili in tema erano l'implementazione del metodo FTCS e BTCS.
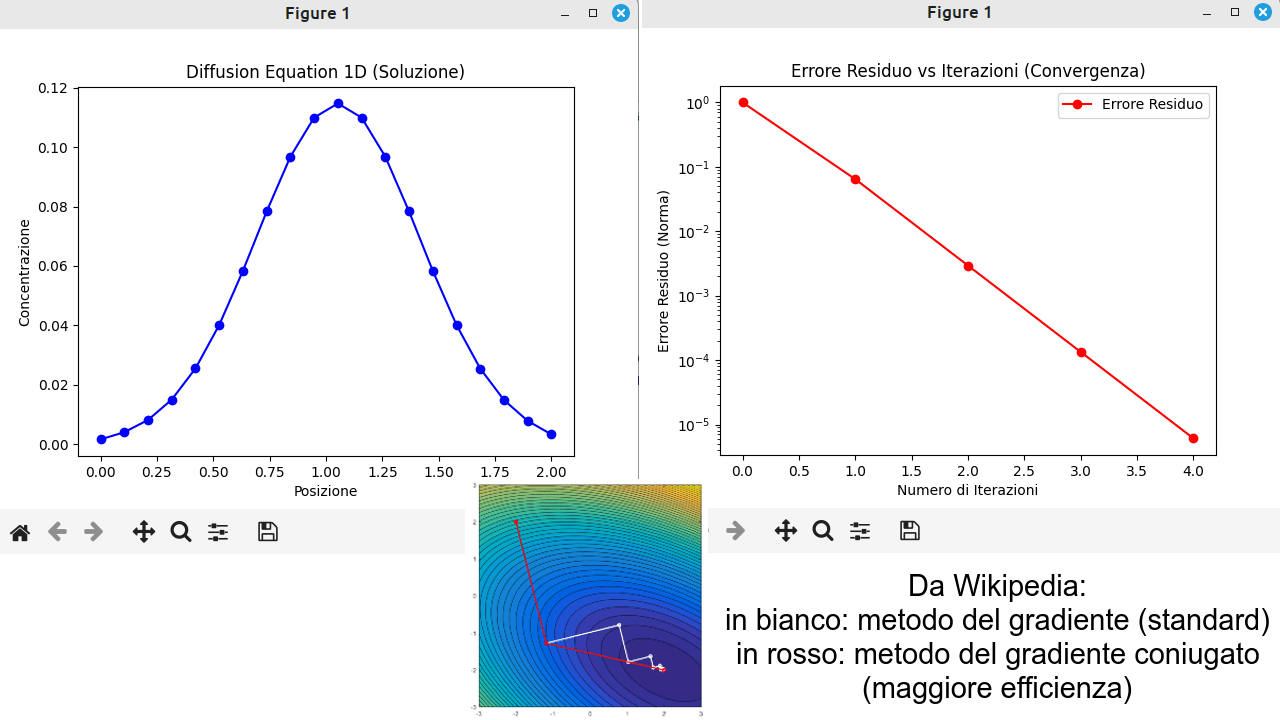
Nel caso specifico, abbiamo l'equazione della diffusione (equazione matematica, poi l'applicazione fisica a piacere, che sia diffusione termica, di una sostanza inquinante non reattiva, ecc). Quindi ho creato un problema di esempio, con dati di esempio e implementato questo algoritmo matematico in linguaggio Python. Dopo tot iterazioni, stampa del grafico (andamento a gaussiana, dalla condizione iniziale con picco localizzato, la diffusione nello spazio, al passare del numero di iterazioni e quindi del tempo, da origine ad una curva di tipo gaussiano, che pian piano si attenua) e stampa dell'errore, su scala logaritmica! Questo per vedere un andamento lineare (o circa lineare), altrimenti il decadimento dell'errore sarebbe esponenziale, il che dimostra l'efficienza di questo metodo numerico.
Vediamo quindi il codice Python, con alcuni commenti per rendere più comprensibili i passaggi.
# Diffusion Equation 1D - Metodo del Gradiente Coniugato
import numpy as np
import matplotlib.pyplot as plt
# Parametri del problema
V0 = 1.0 #valore picco iniziale
L = 2.0 # lunghezza del dominio
T = 0.25 # tempo totale di simulazione
D = 0.25 # coefficiente di diffusione
dx = 0.1 # passo discretizzazione spaziale
N = int(L / dx) # numero di punti spaziali
delta = 0.05 # passo di discretizzazione numerica
dt = 1.0 * delta * dx**2 / D # passo discretizzazione temporale
time_steps = int(T / dt) # numero di passi temporali
# Matrice A e vettore b
A = np.zeros((N, N))
b = np.zeros(N)
b[int(N / 2)] = V0 # condizione iniziale, al centro
solution = np.zeros(N)
for j in range(N):
for i in range(N):
if i == j:
A[i, j] = 1 + 2 * delta
elif (i + 1 == j and i < N - 1) or (i - 1 == j and i > 0):
A[i, j] = -delta
def conjugate_gradient(A, b, tol=1e-4, max_iter=1000):
x = np.zeros(len(b))
r = b - A @ x
p = r.copy()
error_residuals = [np.linalg.norm(r)]
for i in range(max_iter):
Ap = A @ p
alpha = r @ r / (p @ Ap)
x += alpha * p
r_new = r - alpha * Ap
error_residuals.append(np.linalg.norm(r_new)) # registra norma dell'errore residuo
if np.linalg.norm(r_new) < tol: # controllo convergenza
break
beta = (r_new @ r_new) / (r @ r)
p = r_new + beta * p
r = r_new
return x, error_residuals
# Risolve il sistema e salva l'errore residuo
solution, error_residuals = conjugate_gradient(A, b)
# Ciclo temporale
for t in range(time_steps):
solution, _ = conjugate_gradient(A, b)
b = solution.copy() # aggiorna b con la soluzione attuale
# Plot finale della soluzione
plt.figure()
x_values = np.linspace(0, L, N)
plt.plot(x_values, solution, 'o-', color='blue')
plt.title("Diffusion Equation 1D (Soluzione)")
plt.xlabel("Posizione")
plt.ylabel("Concentrazione")
plt.show()
# Plot dell'errore residuo
plt.figure()
plt.plot(error_residuals, 'o-', color='red', label="Errore Residuo")
plt.title("Errore Residuo vs Iterazioni (Convergenza)")
plt.xlabel("Numero di Iterazioni")
plt.ylabel("Errore Residuo (Norma)")
plt.yscale('log') # Scala logaritmica per evidenziare l'andamento lineare
plt.legend()
plt.show()
Ecco infine il risultato grafico: soluzione a sinistra, errore residuo in scala logaritmica a destra, in basso ho aggiunto una raffigurazione di Wikipedia che mostra il confronto fra il metodo del gradiente (standard) e il metodo del gradiente coniugato, quest'ultimo più efficiente, converge più rapidamente alla soluzione esatta (errore residuo che cala più velocemente).
Vi piace? Cosa ne pensate? 🙂