Probabilmente almeno per "sentito dire", tutti conoscono l'effetto tunnel (quantum tunnelling) della meccanica quantistica. Secondo la "semplificazione classica", diciamo, nella pratica sufficientemente valida per il mondo macroscopico a cui siamo abituati, questo non ha un equivalente. In termini molto semplici, l'effetto tunnel quantistico indica che una particella, pur avendo energia inferiore a quella richiesta per superare una certa barriera ("barriera di potenziale", di fatto un ostacolo da superare), ha comunque una probabilità diversa da zero di superarla (un equivalente classico, sarebbe come dire che corri contro un muro e hai una probabilità - piccola ma sempre maggiore di zero - di riuscire a passare oltre il muro, riferimento al "binario 9 e 3/4" di Harry Potter). A livello intuitivo, immaginiamo ad esempio la maglia di un filtro, un corpo macroscopico NON è un continuum ma un "sistema" formato da tantissime particelle, quindi se prendiamo una singola particella, può anche passare attraverso la maglia di un filtro, se invece pretendiamo che passino tutte le particelle, per una certa profondità (deve sempre "prendere il buco"), la cosa diventa estremamente improbabile. Perdonatemi l'esempio molto terra-terra, ma almeno rende l'idea.
Vediamo prima un'animazione di esempio, tratta da Wikipedia.

Quello che ho deciso di fare è, partendo dalla matematica che ci sta dietro, ricostruire i vari passaggi (mi riferisco all'interpretazione tradizionale probabilistica della meccanica quantistica, non varianti come quella di David Bohm, ecc) e fornire quindi una mia interpretazione, per cercare poi di spiegarla in modo semplice. Sostituendo alcuni numeri, vediamo anche degli esempi.
Devo comunque partire dalle formule matematiche, non spaventatevi e semmai passate alla parte di spiegazione più "terra-terra". Spiego la procedura e le questioni principali, in punti.
- equazione di Schrödinger, caso generale 3D e non stazionario (∂/∂t≠0), poi caso 1D:


- ipotesi di stazionarietà, indipendente dal tempo: ∂/∂t=0, si elimina il primo membro dell'equazione
- Ψ=funzione d'onda (prendiamolo così, non ci occorre aggiungere altro)
- h=costante di Planck = 6,62607015 * 10-34 J*s, è un numero piccolissimo!!
- ħ=h/(2π), costante di Planck ridotta (divisa per 2pigreco)
- m=massa della particella
- V=energia potenziale (della "barriera di potenziale" che si vuole superare)
- x=coordinata, direzione di moto (mi scontro con una barriera di potenziale, cercando di proseguire per un tratto di lunghezza pari a x)
- P(x)=Ψ(x)2: semplificando diciamo che nel nostro caso Ψ2 è uguale alla probabilità di riuscire ad avanzare lungo x, con le condizioni che abbiamo imposto (barriera di potenziale, massa della particella, ecc)
- coefficienti costanti: posso ricavare per via analitica la soluzione dell'equazione di Schrödinger, che avrà questa forma: Ψ(x)=C1e√k*x+C2e-√k*x, C1 e C2 costanti da determinare
- indico con k=2mV/ħ2
- x=0 abbiamo Ψ=1, situazione iniziale nota e analogamente P=1 (ovvero 100%), infatti se x=0 devo ancora superare il muro, quindi C1+C2=1
- x-->∞, questa condizione indica che tendendo ad infinito devo avere Ψ=0 e P=0 (infatti probabilità che per forza di cose tende a zero se provo a superare per una distanza infinita una barriera), questo deve annullare il primo termine che altrimenti diverge quindi C1=0 e, essendo C2=1-C1, C2=1
- quindi sostituisco: Ψ(x)=e-√k*x, ha la forma di un esponenziale decrescente, come giusto che sia
- con questo esempio, quindi risulta: P(x)=Ψ(x)2=e-2√k*x
- verifiche: ∂P/∂x<0, ∂P/∂m<0, ∂P/∂V<0, concettualmente tutto torna
Ecco, la trattazione matematica è stata spiegata (se l'avete letta oppure saltata, in ogni caso eccoci qui). Nel mondo microscopico l'effetto tunnel trova effettivamente applicazione; nel mondo macroscopico invece, viste le dimensioni dei numeri in gioco (come detto, la forma è quella di un esponenziale decrescente!!), la probabilità di successo sarà del tutto trascurabile, sarebbe irrealistico pensare il contrario, però attenzione, in senso stretto non è comunque zero. Il passaggio da mondo microscopico a mondo macroscopico è un continuum, non c'è una soglia netta!
Vediamo ora degli esempi numerici, giusto per avere un'idea indicativa della grandezza delle variabili in gioco.
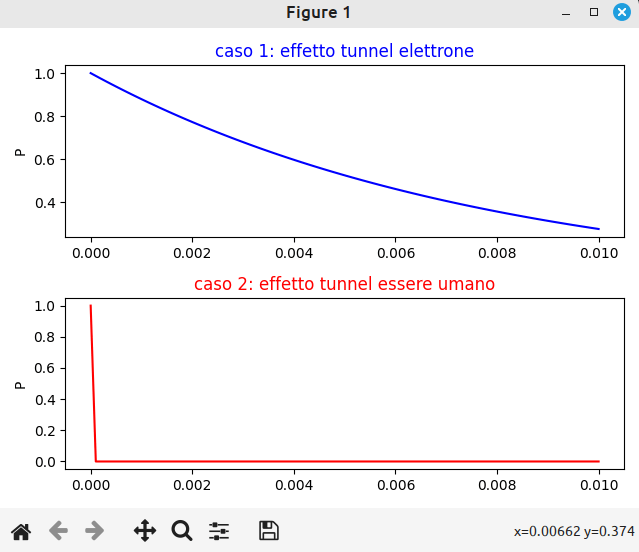
- caso 1: elettrone, dato che ho considerato una distanza massima decisamente enorme per un elettrone, ovvero 1cm, ho preso un valore di potenziale (barriera di potenziale) estremamente basso (altrimenti la probabilità sarebbe ovunque prossima allo zero)
- caso 2: essere umano, considerando sempre profondità di 1cm, peso 60kg, come barriera di potenziale prendo un valore di esempio 100J: vediamo subito che la probabilità è prossima allo zero (sempre 1 per x=0 dato che deve ancora oltrepassare la barriera, ma la probabilità crolla subito, a differenza di prima).
Codice di esempio in Python:
from matplotlib import pyplot as plt
import numpy as np
def P(x,m,V):
h_red=6.62607015 * 10**(-34) #[J*s]
k=2*m*V/(h_red**2)
#m=[kg]
#V=[J=N*m]
return np.exp(-2*np.sqrt(k)*x)
x=np.linspace(0,0.01,100)
fig,ax=plt.subplots(2,1) #2 grafici
#caso 1 = elettrone
#caso 2 = essere umano
ax[0].set_title("caso 1: effetto tunnel elettrone",color="blue")
ax[1].set_title("caso 2: effetto tunnel essere umano",color="red")
ax[0].plot(x,P(x,9.10938*10**(-31),1e-33),color="blue")
ax[1].plot(x,P(x,60,100),color="red")
ax[0].set_ylabel("P")
ax[1].set_ylabel("P")
plt.tight_layout() #ottimizza gli spazi
plt.show()
Ecco infine un'immagine, con i due grafici degli esempi fatti, a confronto.
Cosa ne pensate? Vi piace? Spero di sì dato che ho impiegato un bel po' a scriverlo! 😁 Spero che almeno la spiegazione di base sia stata semplice e chiara.