Calcolo direttrice parabola

NameNick321

Sia 4x² -4xy + 1 y² + 4x + 8y -4 = 0

Trova la direttrice della parabola:

Ho trovato il vertice V = (1/5; 2/5) e 2x-y=0 asse di simmetria. Come trovo il fuoco e la direttrice?

NameNick321

Giulio_M

NameNick321 non avevo risposto perché nello spefico non ricordo bene le formule, questioni puramente didattiche che ho già rimosso 😁 Faccio però alcune considerazioni.
La seguente funzione in due variabili non riusciamo a renderla esplicita quindi la dobbiamo gestire come f(x,y)=0. Non è semplice stabilire con esattezza il dominio (in x), lo possiamo fare tramite la rappresentazione grafica (nella mia immagine, tralascia i due punti esterni che noon centrano, nel resto vedi l'andamento della parabola, vedi il range di x circa [-1.6;1.6], ad esempio infatti sostituendo x=2 in f(x,y) ottieni un'equazione di secondo grado in y tale per cui Δ=B²-4AC<0 quindi non definita nel campo dei numeri reali.
Metto la rappresentazione grafica e il codice, fatto tramite metodo della bisezione (con qualche lieve variante), algoritmo scritto in Python.

import numpy as np
from matplotlib import pyplot as plt
R=2
N=100
def f(x,y):
    return 4*x**2-4*x*y+y**2+4*x+8*y-4 #f(x,y)=0
def bisezione(N,x,a,b):
    xmin=a
    xmax=b
    for i in range(N):
        if(i==(N-1) and f(x,0.5*(xmin+xmax))**2>0.1):
            return None
        if(f(x,0.5*(xmin+xmax))**2<1e-6):
            break
        else:
            if(f(x,0.5*(xmin+xmax))*f(x,xmin)<0):
                xmax=0.5*(xmin+xmax)
            elif(f(x,0.5*(xmin+xmax))*f(x,xmax)<0):
                xmin=0.5*(xmin+xmax)
    return 0.5*(xmin+xmax)
plt.figure()
for i in range(N):
    if(bisezione(50,-R+2.0*(i+1)*R/N,-100,100) != None):
        plt.plot(-R+2.0*(i+1)*R/N,bisezione(50,-R+2.0*(i+1)*R/N,-100,100),'o',color="blue")
plt.title("f(x,y)=4x^2-4xy+y^2+4x+8y-4=0")
plt.show()

grafico-funzione-due-variabili-parabola-python-matplotlib

Averne la visualizzazione grafica spero comunque che possa essere utile per procedere con il resto (ripeto, non scontata dato che se non la riesci a scrivere in forma esplicita, occorre risolverla per via implicita con un metodo come la bisezione, come ho fatto io).

magomerlino

NameNick321

Il procedimento che segue va sotto il nome di "riduzione di una conica a forma canonica" ed è uno standard nel corso di "Geometria ed Algebra Lineare", che in genere si tiene al primo o secondo anno di matematica, fisica od ingegneria.

Dunque, assegnata la conica di equazione cartesiana (*):

4x² - 4xy + y² + 4x + 8y - 4 = 0

individuiamo la matrice dei termini quadratici:

[4 -2]
[-2 1]

e calcoliamo i rispettivi autovalori e autovettori normalizzati:

λ1 = 5
v1 = [2/√5, -1/√5]

λ2 = 0
v2 = [1/√5, 2/√5]

Ciò fatto, applichiamo il seguente cambiamento di coordinate:

x = 2X/√5 + Y/√5
y = -X/√5 + 2Y/√5

che sostituite in (*) porgono:

5X² + 4√5Y - 4 = 0

ossia:

5X² + 4√5(Y - 1/√5) = 0.

Ciò fatto, applichiamo quest'altro cambiamento di coordinate:

x' = X
y' = Y - 1/√5

ossia, invertendo il precedente cambiamento di coordinate, otteniamo:

x' = 2x/√5 - y/√5
y' = x/√5 + 2y/√5 - 1/√5

ossia, invertendo anche quest'ultimo cambiamento di coordinate, otteniamo:

x = 1/5 + 2x'/√5 + y'/√5
y = 2/5 - x'/√5 + 2y'/√5

che sostituite in (*) porgono:

5x'² + 4√5y' = 0

ossia:

y' = (-√5/4)x'²

che è l'equazione cartesiana di una parabola in forma canonica.

Pertanto, nel sistema di riferimento rototraslato O'x'y', banalmente:

vertice: V'(0, 0);
fuoco: F'(0, -1/√5);
asse: x' = 0;
direttrice: y' = 1/√5;

mentre, grazie ai cambiamenti di coordinate di cui sopra, nel sistema di riferimento Oxy:

vertice: V(1/5, 2/5);
fuoco: F(0, 0);
asse: 2x/√5 - y/√5 = 0, ossia: 2x - y = 0.
direttrice: x/√5 + 2y/√5 - 1/√5 = 1/√5, ossia: x + 2y - 2 = 0.

Inoltre, qualora facesse comodo, possiamo anche parametrizzare la parabola:

x = 1/5 + 2t/√5 - t²/4
y = 2/5 - t/√5 - t²/2

in modo tale che facendo variare t ∈ R si possano plottare tutti i suoi punti:

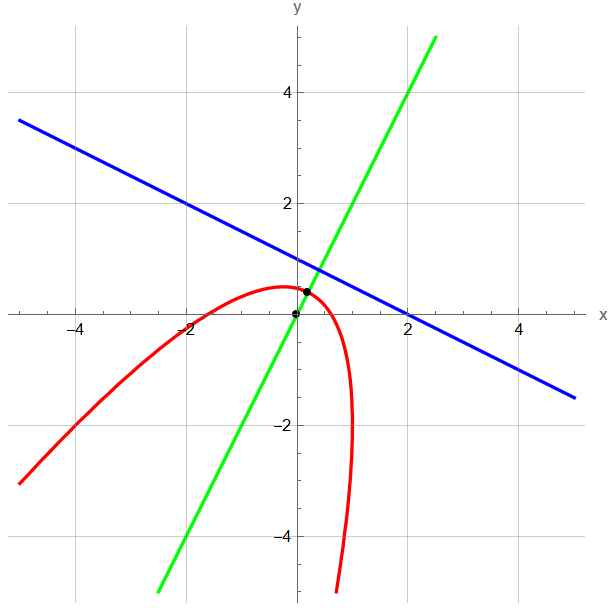
Buono studio, ciao!