user1972 i numeri complessi nascono dall'esigenza di estendere la validità a problemi matematici da trattare, vale a dire che abbiamo:
- numeri naturali (interi positivi)
- numeri interi (altrimenti non riusciamo a gestire numeri come -1)
- numeri razionali (i numeri interi non bastano, se voglio studiare ad esempio 0,5)
- numeri reali (razionali + irrazionali, ad esempio π non è esprimibile sotto forma di moltiplicazione o rapporto)
- numeri complessi (se ho x2+1=0, cosa faccio? Butto via l'esercizio oppure definisco l'unità immaginaria i=√-1 e andiamo avanti? La seconda strada permette di andare avanti con lo studio)
Il campo complesso quindi è la più grande e generale estensione di validità.
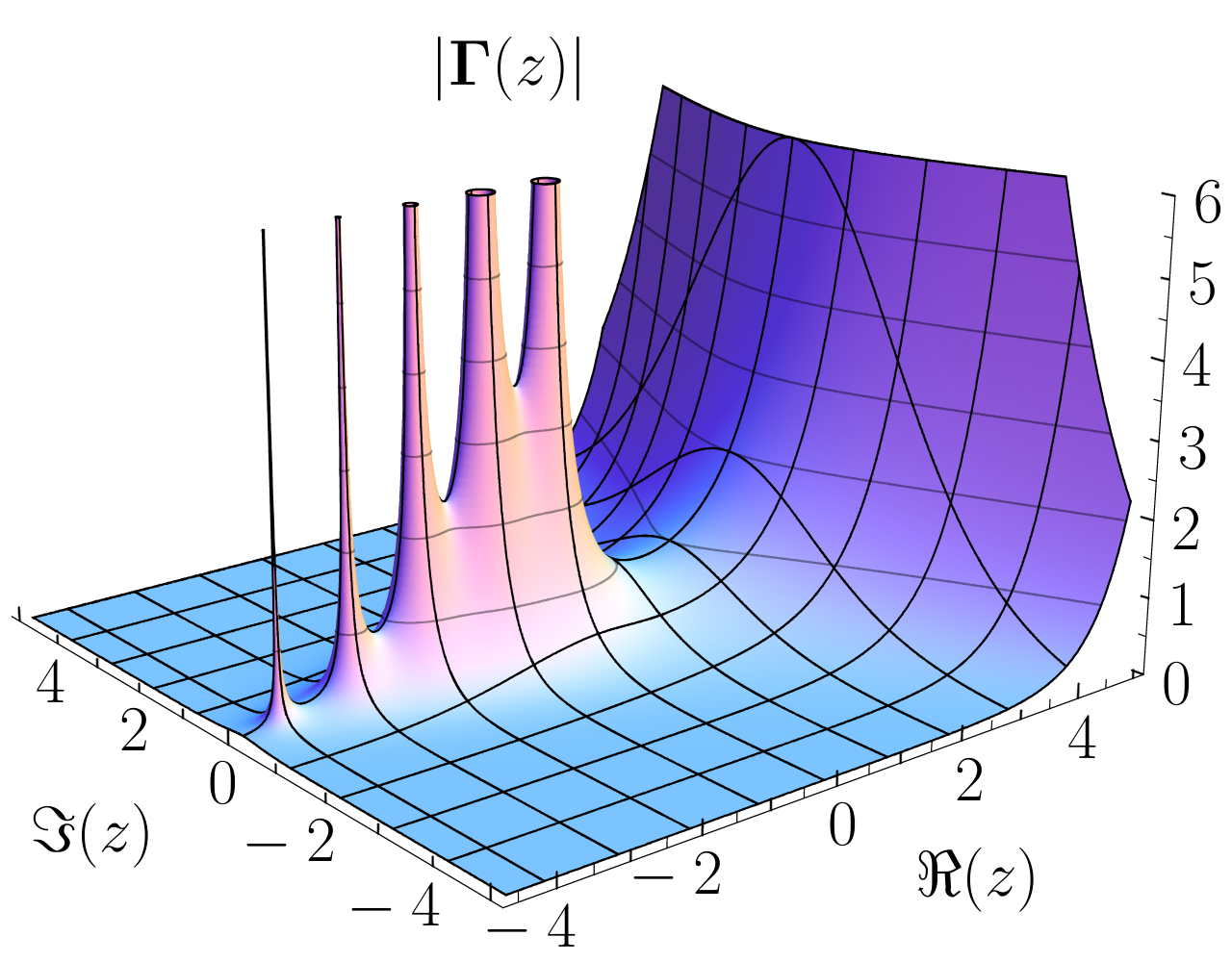
L'analisi complessa è il campo dell'analisi matematica che lavora con funzioni complesse (quindi il caso più generale dell'analisi matematica, che di solito si studia in campo reale).
Una curiosità: i numeri complessi di solito vengono rappresentati sul Piano di Gauss (asse delle ascisse Re(z), asse delle ordinate Im(z), avendo indicato con z il numero complesso). Nei casi in cui volessimo rappresentare una certa f(z), anziché avere un grafico di fatto tridimensionale (Re(z), Im(z), f(z) si può rappresentare con i colori, scala di grigi o diversa tonalità l'andamento della funzione. La cosa si può fare anche con funzioni in campo reale 8vedi il mio esempio: Python - Matplotlib - Heatmap: un grafico bello "visual"), diciamo però che nell'analisi complessa è qualcosa che si nota spesso, ad esempio se cerchi "analisi complessa" compaiono immagini di questo genere (se poi la devi studiare, forse non ti sembra più così bella e colorata 😅). Vediamo due immagini di esempio, di diversa rappresentazione di funzioni complesse, la prima tramite heatmap, la seconda tramite grafico 3D.