Giusto per riempire un po' la nuova sezione di chimica e biologia (anziché metterlo in computer e internet), riporto questo esempio della legge di Gompertz che, simile alla funzione logistica descrive la crescita di una popolazione, in particolare caratterizzata da:
- valore iniziale: X0
- valore finale asintotico (ad esempio a causa della scarsità di risorse): K
- popolazione al tempo t: X(t)
- tasso di crescita: r
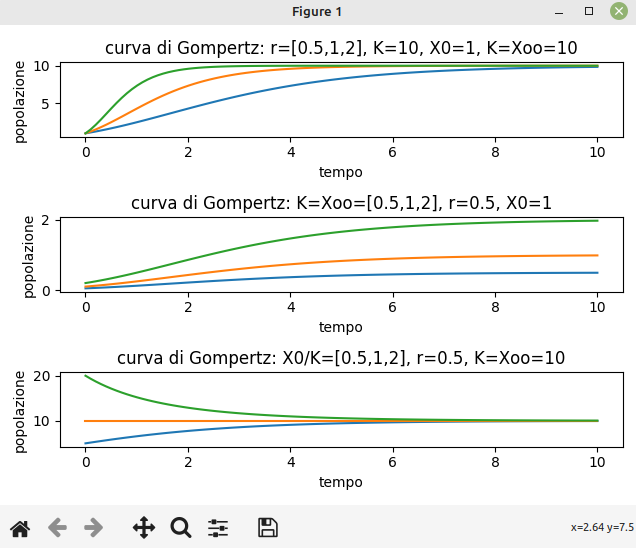
Con un codice scritto in Python e dei valori di esempio, mostriamo anche l'andamento grafico, in questi tre casi (i tre grafici mostrati nell'immagine che segue):
- caso 1: variazione del tasso di crescita
- caso 2: variazione del valore finale, asintotico
- caso 3: variazione del rapporto X0/K ovvero:
- X0>K: equilibrio instabile, non ci sono risorse sufficienti (vari fattori limitanti dell'ambiente) quindi la popolazione decresce
- X0=K: situazione già di equilibrio
- X0<K: aumenta fino alla tendenza asintotica di K
Riportiamo ora il codice:
import numpy as np
from matplotlib import pyplot as plt
#dXdt=-rXln(X/K)
#X=popolazione
K=10 #Xmax
X0=1
r=0.5 #tasso di crescita
Tmax=10
t=np.linspace(0,Tmax,100)
fig,ax=plt.subplots(3) #3 grafici
C=np.log(X0/K)
for i in range(3): #variazione di r
ax[0].plot(t,K*np.exp(C*np.exp(-r*t)))
r*=2
r=0.5
K=0.5
for i in range(3): #variazione di K
ax[1].plot(t,K*np.exp(C*np.exp(-r*t)))
K*=2
K=10
X0=0.5*K
for i in range(3): #variazione di X0/K
C=np.log(X0/K)
ax[2].plot(t,K*np.exp(C*np.exp(-r*t)))
X0*=2
ax[0].set_title("curva di Gompertz: r=[0.5,1,2], K=10, X0=1, K=Xoo=10")
ax[1].set_title("curva di Gompertz: K=Xoo=[0.5,1,2], r=0.5, X0=1")
ax[2].set_title("curva di Gompertz: X0/K=[0.5,1,2], r=0.5, K=Xoo=10")
for i in range(3):
ax[i].set_xlabel("tempo")
ax[i].set_ylabel("popolazione")
plt.tight_layout() #ottimizza gli spazi
plt.show()
Infine l'immagine per mostrare i tre grafici.
Conoscevate la funzione di Gompertz e la curva logistica? Cosa ne pensate? Qualcosa da aggiungere? 🙂