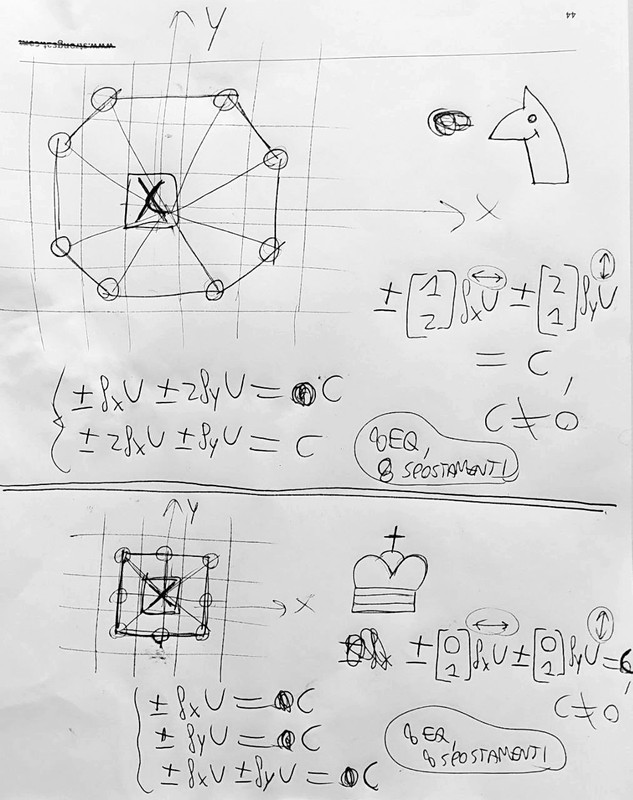
Per caso stavo pensando alle mosse degli scacchi, approfondendo in particolare il caso del cavallo (il pezzo più interessante, per come muove) e poi il re. Partendo da una cella centrale, ipotizzando che non ci siano vincoli come altri pezzi oppure oltre il bordo della scacchiera (quindi, indica le mosse potenzialmente valide in generale, poi casomai da verificare con altre condizioni), posso segnare le celle in cui il pezzo potrebbe muoversi, con l'ipotesi quindi di libertà. Il cavallo dà origine ad un ottagono, il re ad un quadrato, come vediamo nel'immagine alla fine.
Ho poi pensato di scriverlo in forma differenziale, coordinate X e Y come indicato, per entrambi i casi un totale di 8 equazioni, quindi 8 spostamenti. Questo in realtà indicherebbe il percorso (nel disegno, linee oblique) quindi il collegamento fra la cella centrale, punto partenza e una delle celle di arrivo (quindi un'ipotetica mossa valida per quel pezzo). Per evitare che coincidano metà delle equazioni (-- e ++), l'ho messo uguale ad una costante che deve essere diversa da zero.
Concettualmente ho pensato di scrivere questa cosa, a livello teorico ok, faccio fatica ad immaginarlo come risvolto pratico, diciamo un possibile significato che vada oltre la validità della singola mossa. In particolare sarebbe interessante combinare l'interazione di più pezzi, anche se risulta complicata da impostare. Il risvolto sarebbe tutt'altro che banale, rendere deterministico e non probabilistico un possibile algoritmo sulle mosse da seguire.
In generale, cosa ne pensate? Quantomeno riguardo alle figure geometriche, ci avevate mai pensato?
Ecco l'immagine: