Ok, titolo un pochino provocatorio e ironico, ma volevo fare qualche considerazione e un semplice esempio numerico. Cerco di stare sul leggero e divertente, perché oggi dopo una gara di corsa, oltre alle gambe ho anche il cervello stanco. Giorni fa avevo già parlato di idrodinamica, correnti a pelo libero e in particolare il fenomeno del risalto idraulico.
Oggi ragioniamo su questa ipotetica situazione: fiume, andamento molto rettilineo, canalizzato, si può studiare il cosiddetto moto uniforme, studio delle correnti a pelo libero, formule empiriche dell'idrodinamica (approfondimento). A lato del fiume, poco oltre l'argine, c'è il nostro orto che vogliamo irrigare, solo che c'è siccità, l'acqua costa... Troviamo una soluzione alternativa! 😁
L'altezza di moto uniforme (in parole semplici, il livello dell'acqua) è data da questa formula:
y=(Q/(ks * b * if0.5))3/5, con l'approssimazione b>>y cioè fiume molto più largo che alto
L'altezza critica (yc) in questo caso non ci interessa mentre diventava utile per studiare il caso del risalto idraulico.
Prendiamo questi dati iniziali:
- Q = 100 m3/s
- b = 20 m
- pendenza (if) = 0.001 = 0,1%
- ks = 40
Con questi valori: yc=1,37m, yu=2,28m (il valore che ci interessa). Supponiamo che l'argine sia a 4m, quindi per irrigare il nostro bellissimo orto, dobbiamo alzare il livello yu oltre i 4m.
ks è un parametro empirico, la "scabrezza del fondo", più è alto e più è liscio, diciamo crea meno attrito quindi ne consegue che il livello è più basso (approfondimento). Perfettamente liscio, roba da laboratorio, supera i 100-110, altrimenti un classico canale 30-40, un fiume a seconda delle irregolarità (sassi, vegetazione ecc) può arrivare anche sotto il 20.
Quindi studiamo le possibilità: come irrigare il nostro orticello gratis? Dobbiamo provocare l'aumento di livello del moto uniforme! Dalla formula precedente, dato che la portata del fiume non riusciamo a cambiarla, le possibilità sono:
- restringere la base (riporto di materiale creando una zona sufficientemente lunga con questo restringimento costante)
- diminuire la pendenza (riporto di materiale su livelli diversi, piuttosto complicato da fare)
- abbassare l'argine (va beh, intervento pesante e distruttivo anche questo)
- diminuire ks: evviva, basta buttare tanti "sassolini" sul fondo, un insieme di materiale da creare maggiore attrito!
La soluzione migliore e più semplice quindi è diminuire ks aumentando l'irregolarità del fondo. Mantendendo i valori di prima e avendo portato ks a 15 (prima era 40), si ottiene yu=4,11m. Maggiore di 4m quindi siamo riusciti nel nostro scopo, irrigare gratis!
Si può fare? Mah, diciamo che è difficile essere scoperti 😁 voi nascondete bene il libro di idrodinamica! Agire sulla scabrezza del fondo ("buttare sassolini") è ben più comodo rispetto alle altre opzioni, larghezza e pendenza del fondo.
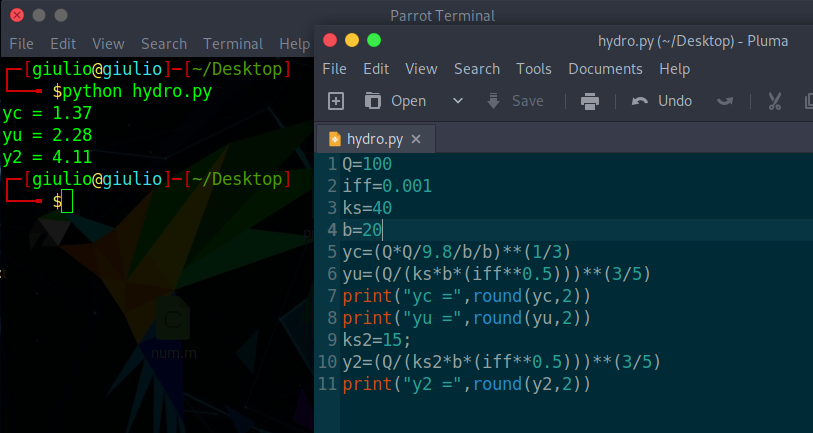
Cosa ne pensate? Vi metto lo screenshot di un semplice programmino in Python che mostra i risultati.