Bobi statica, quindi dobbiamo rispettare le seguenti condizioni di equilibrio:
L'aspetto chiave è questo:
- se il centro di massa (della superficie piana del mattone, in questo caso) si trova allineato in x con il punto che poggia a terra, allora è in equilibrio (caso teorico, nella pratica una situazione di questo tipo è ovviamente un equilibrio instabile, punto massimo dell'energia potenziale ovvero ∇=0, ∇2<0); in tal caso abbiamo:
- ƩFx=0 --> non ci sono forze orizzontali
- ƩFy=0 --> Va-mg=0 --> Va=mg, dove Va è la reazione vincolare di contatto col terreno (va beh mi sono accorto dopo che potevo chiamarlo Vb anziché Va essendo nominato B il contatto al suolo, il concetto comunque è questo)
- ƩM=0 --> non ho azione flettente, non c'è eccentricità, avrei braccio nullo
- se il centro di massa non si trova allineato in x con il punto di contatto a terra, allora NON è in equilibrio, l'eccentricità determina un braccio (una lunghezza) che moltiplicata per una forza (in questo caso mg, il peso proprio) determina un'azione flettente, M=mgε), quindi:
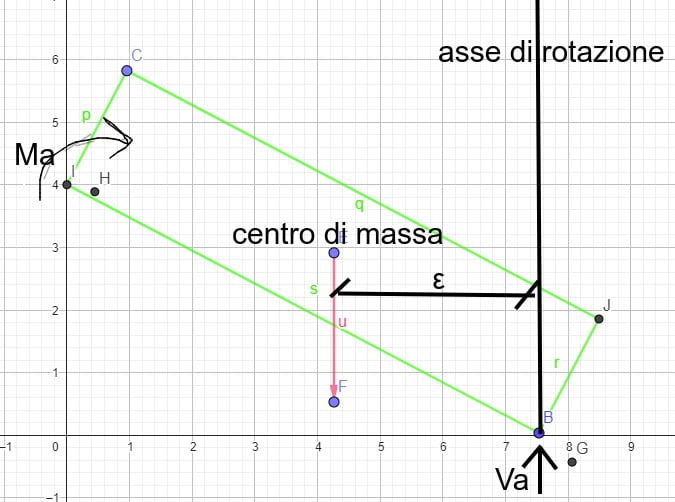
- ho indicato con ε l'eccentricità che nello specifico è il segmento parallelo ad x, fra il centro di massa e l'intersezione con la verticale passante per il punto di appoggio (NB segmento orizzontale, parallelo al suolo, NON inclinato come la posizione attuale del mattone!)
- ƩFx=0 --> non ci sono forze orizzontali
- ƩFy=0 --> Va-mg=0 --> Va=mg, dove Va è la reazione vincolare di contatto col terreno
- ƩM=0 --> prendo come polo il punto di contatto al suolo, per comodità: quindi Ma-mgε=0 --> Ma=mgε (analogamente a prima, l'ho chiamato Ma, potevo chiamarlo Mi dato che il punto di contatto con la parete si chiama I)
Noi siamo chiaramente nel secondo caso, centro di massa non allineato in x col punto di contatto a terra e quindi è presente un'azione flettente quindi la parete deve bloccare la rotazione. La cosa è anche intuitiva, se infatti non ci fosse la parete, il corpo non sarebbe più in equilibrio ma ruoterebbe a causa dell'azione flettente pari a mgε, fino ad appoggiarsi per intero al terreno.
Modifico l'immagine che hai linkato, inserendo i simboli che ho definito, in modo che sia più chiaro 🙂