Dopo aver visto l'esempio Calcolo Pi Greco: una nuova formula più efficiente, vediamo un caso diverso, ho creato questo algoritmo (e relativo programma in C):
- definisco una costante, ad esempio la costante di Planck ridotta (fra parentesi, qualsi sempre lo chiamavo Plank e non Planck 😅) ovvero
h/(2π) = 6.62607015 * 10^(-34) / (2π) J*s, che approssimata alla 50° cifra decimale risulta pari a 1.05457181764615648411620441038394346833229064941406
- prendo spunto dalla Formula di Bailey–Borwein–Plouffe come per l'altro caso che avevo linkato, in particolare dalla formula generale:

farei una cosa del tipo: sum( (1/16)^k * (Ak^3+Bk^2+Ck+D)/(Ek^4+Fk^3+Gk^2+H*k+I) )
- determino i coefficienti A,B,C,D,E,F,G,H,I tramite una variante del metodo della bisezione
- trovo un giusto compromesso nel numero di iterazioni (sia per la variante generale della formula BBP, sia per la convergenza della bisezione) e anche per il range di partenza per ogni coefficiente da determinare, necessario per implementare la bisezione
- varie ottimizzazioni del codice
Come risultato ho trovato una formula accurata fino alla quattordicesima cifra decimale (più che altro qui dipende molto dall'approssimazione di Pi Greco, dato che poi per il resto abbiamo ℏ=h/(2π).
I coefficienti che ho trovato, secondo la formula scritta prima, risultano pari a:
A=11; B=6; C=11; D=5.94; E=11; F=11; G=11; H=11; I=5.88
Ecco tutto il codice in C (ad un certo punto sembra molto contorto e incasinato, lo so 😅):
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N 50
#define PI 3.14159265358979323846264338327950288419716939937510 //50cifre
#define hrid 6.62607015/(2*PI) //costante di plank ridotta (*1e-34 Js)
typedef struct{
long double a,b,c,d,e,f,g,h,i;
}var;
long double f(unsigned char n, long double A, long double B, long double C, long double D, long double E, long double F, long double G, long double H, long double I);
var bisezione(unsigned char niter, long double Amin, long double Amax, long double Bmin, long double Bmax, long double Cmin, long double Cmax, long double Dmin, long double Dmax, long double Emin,long double Emax, long double Fmin, long double Fmax, long double Gmin, long double Gmax, long double Hmin, long double Hmax, long double Imin, double Imax);
int main() {
register long double sum=0;
register long double A,B,C,D,E,F,G,H,I;
A=1.0;B=1.0;C=1.0;D=1.0;E=1.0;F=1.0;G=1.0;H=1.0;I=1.0;
long double range=10.0;
var ris;
ris=bisezione(N,A,A+range,B,B+range,C,C+range,D,D+range,E,E+range,F,F+range,G,G+range,H,H+range,I,I+range);
printf("risultati con N=%d\n",N);
printf("A=%.2Lf|B=%.2Lf|C=%.2Lf|D=%.2Lf|E=%.2Lf|F=%.2Lf|G=%.2Lf|H=%.2Lf|I=%.2Lf\n",ris.a,ris.b,ris.c,ris.d,ris.e,ris.f,ris.g,ris.h,ris.i);
printf("f_Giulio_M = %.50Lf\n",f(N,ris.a,ris.b,ris.c,ris.d,ris.e,ris.f,ris.g,ris.h,ris.i));
printf("h / (2*pi) = %.50f * 10^(-34) J*s\n",hrid);
return 0;
}
long double f(unsigned char n, long double A, long double B, long double C, long double D, long double E, long double F, long double G, long double H, long double I){
long double ris=0;
unsigned char j;
for(j=0;j<n;j++){
ris+=pow(16,-j)*(A*j*j*j+B*j*j+C*j+D)/(E*j*j*j*j+F*j*j*j+G*j*j+H*j+I);
}
return ris;
}
var bisezione(unsigned char niter, long double Amin, long double Amax, long double Bmin, long double Bmax, long double Cmin, long double Cmax, long double Dmin, long double Dmax, long double Emin,long double Emax, long double Fmin, long double Fmax, long double Gmin, long double Gmax, long double Hmin, long double Hmax, long double Imin, double Imax){
var ris;
unsigned char j;
long double x1min=Amin; long double x1max=Amax;
long double x2min=Bmin; long double x2max=Bmax;
long double x3min=Cmin; long double x3max=Cmax;
long double x4min=Dmin; long double x4max=Dmax;
long double x5min=Emin; long double x5max=Emax;
long double x6min=Fmin; long double x6max=Fmax;
long double x7min=Gmin; long double x7max=Gmax;
long double x8min=Hmin; long double x8max=Hmax;
long double x9min=Imin; long double x9max=Imax;
for(j=0;j<niter;j++){
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,x1min,0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x1max=0.5*(x1min+x1max);}else{x1min=0.5*(x1min+x1max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),x2min,0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x2max=0.5*(x2min+x2max);}else{x2min=0.5*(x2min+x2max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),x3min,0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x3max=0.5*(x3min+x3max);}else{x3min=0.5*(x3min+x3max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),x4min,0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x4max=0.5*(x4min+x4max);}else{x4min=0.5*(x4min+x4max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),x5min,0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x5max=0.5*(x5min+x5max);}else{x5min=0.5*(x5min+x5max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),x6min,0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x6max=0.5*(x6min+x6max);}else{x6min=0.5*(x6min+x6max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),x7min,0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)<0){x7max=0.5*(x7min+x7max);}else{x7min=0.5*(x7min+x7max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),x8min,0.5*(x9min+x9max))-hrid)<0){x8max=0.5*(x8min+x8max);}else{x8min=0.5*(x8min+x8max);}
if((f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),0.5*(x9min+x9max))-hrid)*(f(N,0.5*(x1min+x1max),0.5*(x2min+x2max),0.5*(x3min+x3max),0.5*(x4min+x4max),0.5*(x5min+x5max),0.5*(x6min+x6max),0.5*(x7min+x7max),0.5*(x8min+x8max),x9min)-hrid)<0){x9max=0.5*(x9min+x9max);}else{x9min=0.5*(x9min+x9max);}
}
ris.a=0.5*(x1min+x1max);
ris.b=0.5*(x2min+x2max);
ris.c=0.5*(x3min+x3max);
ris.d=0.5*(x4min+x4max);
ris.e=0.5*(x5min+x5max);
ris.f=0.5*(x6min+x6max);
ris.g=0.5*(x7min+x7max);
ris.h=0.5*(x8min+x8max);
ris.i=0.5*(x9min+x9max);
return ris;
}
Vediamo infine un'immagine che mostra il risultato dell'esecuzione, con i parametri impostati arrivo alla quattordicesima cifra decimale.
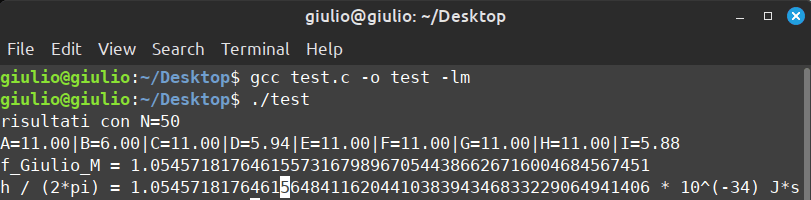
Nel complesso direi che rispetto al caso precedente (approssimazione di Pi Greco), calcolato tramite Newton-Raphson, anche dal punto di vista dell'implementazione, programmazione, questo codice risulta più versatile (se "mi gira", al posto della costante di Planck ridotta, con una piccola modifica posso calcolare altro), necessita di meno controlli e ha maggiore accuratezza (non ha limiti dovuti all'approssimazione numerica della derivata prima, la cui accuratezza risente del numero massimo di cifre decimali possibili per la variabile allocata in memoria).
Cosa ne pensate, vi piace? Vi sembra efficiente? 🙂